Độ dốc và phát hiện cạnh

 Trong ảnh số, những điểm ảnh có độ sáng chênh lệch đột biến so với những điểm ảnh lân cận gọi là các điểm cạnh. Và tập hợp các điểm này tạo nên hình dạng, cấu trúc của đối tượng trong ảnh. Để có thể xác định được vùng điểm cạnh trên tọa độ ảnh, trước hết ta cần tính “gradient” – độ dốc, của ảnh xám. Chúng ta sau đó áp dụng thuật toán Canny – một trong những giải thuật nổi tiếng nhất trong xử lý ảnh về phát hiện cạnh. Giải thuật này gồm 4 bước chính: giảm nhiễu, tính gradient và hướng gradient (sử dụng Sobel chiều ngang và chiều dọc), non-maximum suppression (viết tắt là NMS), và cuối cùng là lọc ngưỡng. Tuy nhiên, chúng ta sẽ không đi chi tiết vào phần toán học ở bài học này mà ta sẽ cùng nhau tìm hiểu về lập trình ứng dụng thực tế qua các ví dụ dưới đây. Bạn đọc có thể tìm hiểu thêm về cơ chế toán học của giải thuật trong chuỗi bài “Toán học trong thị giác máy tính”

1.Laplacian và Sobel

Trước khi vào mới đoạn mã, chúng ta cần hiểu được gradient – độ dốc. Trong xử lý ảnh, độ dốc –gradient, chính là độ dốc về mức ánh sáng – sự thay đổi các giá trị điểm ảnh trong ảnh. Vùng ảnh trơn (smooth) có các điểm ảnh trong vùng ảnh có giá trị gần bằng nhau, do đó khi tính đạo hàm sẽ có kết quả gần bằng 0. Đạo hàm bằng 0 thể hiện không có biến thiên về mức sáng. Điều này có nghĩa rằng độ dốc của các điểm ảnh trong vùng ảnh trơn gần như bằng 0. Đạo hàm dương tại một điểm ảnh thể hiện biến thiên ánh sáng đang ở chiều hướng đi lên, ngược lại, đạo hàm âm tại một điểm ảnh cho biết biến thiên mức sáng đang giảm dần. Như vậy, gradient của ảnh là đạo hàm ảnh.

Quay lại với đoạn mã, dòng 1-9, ta thực hiện tương tự các bài học trước: khai báo thư viện, định nghĩa tham số đầu vào, đọc ảnh chuyển đổi ảnh từ hệ màu RGB thành ảnh xám – dòng 13, và hiển thị ảnh – dòng 14. Khi thực hiện tính toán gradient và các cạnh, chúng ta thường tính toán trên một kênh màu – trong trường hợp này, ta sử dụng ảnh xám. Tuy nhiên, bạn đọc cũng có thể thực hiện trên từng kênh màu của ảnh RGB. Chúng ta sẽ bắt đầu với ví dụ đơn giản nhất là ảnh xám.

Ở dòng 16, chúng ta sử dụng phương thức Laplacian để tính độ lớn của gradient qua hàm cv2.Laplacian. Tham số đầu tiên là bức ảnh xám ta muốn xử lý, và tham số thứ hai là loại dữ liệu cho kết quả trả về. Lý do chúng ta chọn kiểu dữ liệu là 64-bit số thực do quá trình biến đổi màu từ đen thành trắng và ngược lại. Khi chuyển đổi từ đen thành trắng được coi là độ dốc dương, trong khi chuyển từ trắng sang đen là một độ dốc âm. Nếu bạn đọc chưa quên ở bài học tính toán trong ảnh số, chúng ta biết rằng 8-bit số nguyên không biểu thị giá trị âm. Và OpenCV sẽ trả ngưỡng tối đa của khoảng giá trị hoặc Numpy sẽ đếm lại từ đầu khi giá trị vượt biên. Đơn giản hơn, nếu bạn đọc không sử dụng kiểu dữ liệu số thực khi tính độ lớn của gradient thì phần lớn trường hợp, chúng ta sẽ bỏ lỡ các cạnh, đặc biệt là khi chuyển đổi từ màu trắng sang màu đen. Để có thể tìm được tất cả các điểm cạnh, ta sử dụng kiểu dữ liệu số thực, sau đó lấy trị tuyệt đối của giá trị gradient rồi chuyển đổi nó về kiểu nguyên 8-bit dòng 17. Đây là điểm bạn đọc nên chú ý, còn lý giải toán học chúng ta sẽ bàn tới ở chuỗi bài khác. Kết quả của việc tính toán gradient bạn đọc có thể theo dõi dưới đây:

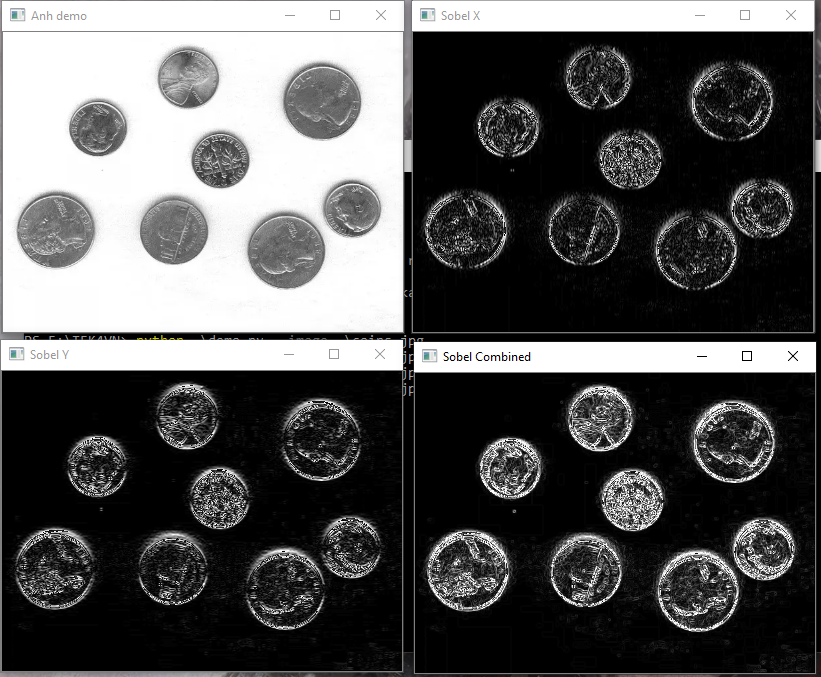
Tiếp theo, chúng ta sẽ tính toán biểu diễn Sobel

Bằng cách sử dụng Sobel, chúng ta có thể tính toán độ lớn gradient biểu diễn theo cả chiều ngang và chiều dọc, cho phép ta tìm cạnh ở cả trục tung và trục hoành. Dòng 20 – 21, phương thức cv2.Sobel nhận tham số đầu tiên là bức ảnh ta muốn xử lý, tiếp đó là kiểu dữ liệu. Hai tham số cuối là đạo hàm theo hai trục tọa độ với giá trị 1, 0 để tìm cạnh theo chiều ngang và ngược lại. Để có thể kết hợp gradient từ cả hai hướng tọa độ, ta sử dụng phép OR. Phép toán bit này trả về True nếu cả hai điểm ảnh lớn hơn 0. Do đó, ta phát hiện được cạnh mà đạo hàm tìm được.

Tuy nhiên, bạn đọc thấy rằng kết quả thu được vẫn còn xuất hiện nhiễu, do đó, chúng sẽ tới với phương pháp tách cạnh Canny.

2.Phương pháp tách cạnh Canny

Để có thể thực hiện phương pháp Canny, trước tiên chúng ta cần khai báo các thư viện sử dụng, đọc ảnh và chuyển đổi ảnh từ hệ màu RGB thành ảnh xám. Sau đó, ta áp dụng phương pháp làm mờ Gaussian để có thể giảm nhiễu từ ảnh. Mục tiêu kết quả cuối cùng là đường viền của đồng xu. Chúng ta thực hiện Canny ở dòng 17 với tham số đầu tiên là ảnh xám cần xử lý, sau đó lần lượt là hai tham số xác định ngưỡng: ngưỡng 1 và ngưỡng 2. Tất cả các giá trị gradient lớn hơn ngưỡng 2 được coi là cạnh. Tất cả giá trị nhỏ hơn ngưỡng 1 không được coi là cạnh, và các giá trị nằm giữa được coi là cạnh hoặc không phải cạnh phụ thuộc vào cách các điểm ảnh kết nối theo tần suất lớn hay nhỏ. Cuối cùng, chúng ta thu được kết quả ở dòng 18

Như vậy, chúng ta thấy rằng ảnh bên trái là ảnh xám cần xử lý sau khi áp dụng phương pháp làm mờ Gaussian và ảnh bên phải là kết quả sau khi sử dụng canny. Phương pháp Canny thu về các đường viền bao đồng xu hiển thị rõ ràng. Ở bài tiếp theo, chúng ta sẽ cùng nhau ứng dụng phương pháp tách cạnh Canny để đếm số đồng xu xuất hiện trong ảnh